APPLICATIONS
Mathematical Applications provides students with mathematical and statistical experience that builds on the three strands of the F-10 curriculum.
Students solve problems in contexts of financial modelling, geometric and trigonometric analysis, graphical and network analysis, and growth and decay in sequences. It provides opportunities to develop systematic strategies that involve analysing univariate and bivariate data, including time series data.
Course Patterns
Students can complete a Major or a Minor. The units are sequential.
Units can be combined with Methods or Specialist Methods to create a Major, Major/ Minor, or Double Major called Further Mathematics.
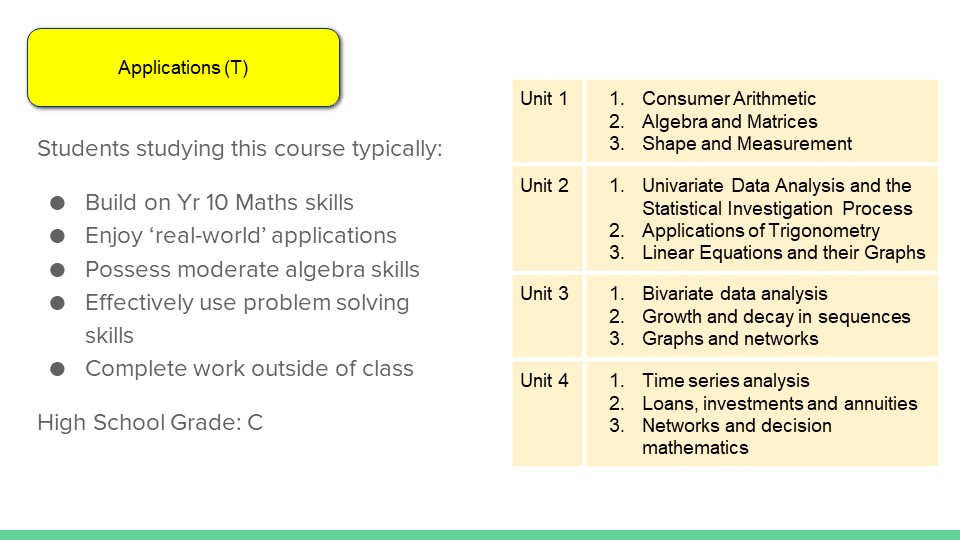
Unit 1
Topic 1: Consumer Arithmetic
Topic 2: Algebra and Matrices
Topic 3: Shape and Measurement
Reviews the concepts of rate and percentage change in the context of earning and managing money. Continues the F-10 study of algebra and introduces matrices. Extends the F-10 curriculum with the concept of similarity and associated calculations involving geometric shapes. The emphasis is on applying these skills in practical contexts, including those involving three-dimensional shapes.
Unit 2
Topic 1: Univariate Data Analysis and the Statistical Investigation Process
Topic 2: Applications of Trigonometry
Topic 3: Linear Equations and their Graphs
Develops students’ ability to organise and proportions in two-outcome populations & summarise univariate data. Extends students’ knowledge of trigonometry to solve practical problems involving non-right-angled triangles in both two and three dimensions, including problems involving the use of angles of elevation and depression, and bearings. Uses linear equations and straight-line graphs, as well as linear-piecewise and step graphs, to model and analyse practical situations.
Unit 3
Topic 1: Bivariate data analysis
Topic 2: Growth and decay in sequences
Topic 3: Graphs and networks
Introduces methods for identifying, analysing and describing associations between pairs of variables, including the least squares method as a tool for modelling and analysing linear associations. Uses recursion to generate sequences to model and investigate patterns of growth and decay in discrete situations. These are applied in practical situations, including modelling the growth of compound interest, populations or the decrease in the value of a car over time. . The language of graphs and the way in which graphs, represented as a collection of points and interconnecting lines, can be used to analyse everyday situations such as rail or social networks.
Unit 4
Topic 1: Time series analysis
Topic 2: Loans, investments and annuities
Topic 3: Networks and decision mathematics Introduces the concepts and techniques of time series. Aims to solve practical problems associated with taking out or refinancing a mortgage and making investments. Uses networks to model and aid decision making in practical situations.