SPECIALIST METHODS
Specialist Methods focuses on the development of the use of calculus and statistical analysis. The course has a challenging level of algebra, so it is expected that students are confident and capable in the algebra skills of the Australian Curriculum 10A course (or equivalent).
Course Patterns
Students can complete a major or a minor. This course is sequential. Students can complete a major-minor or double major in Specialist Mathematics by studying Specialist Methods in conjunction with Specialist Mathematics (only).
Unit 1
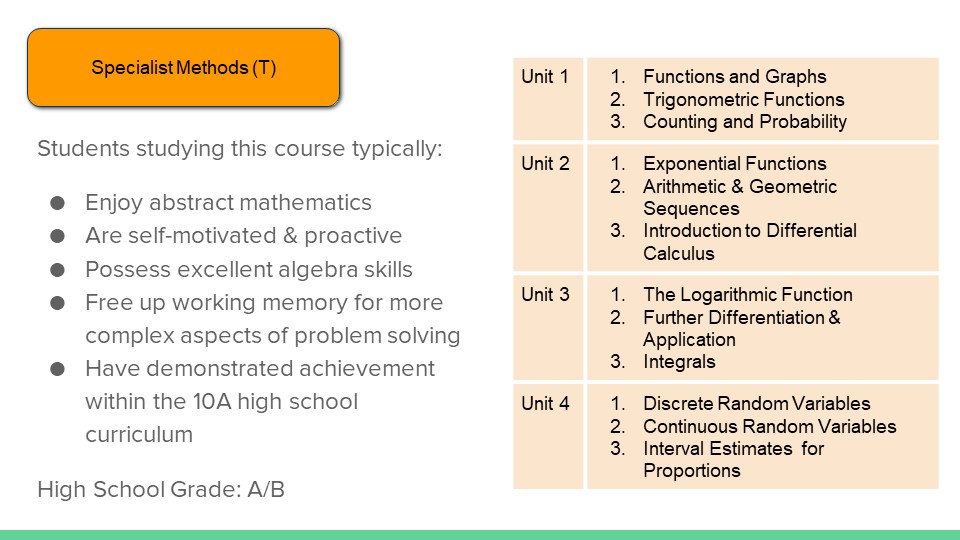
Topic 1: Functions and Graphs
Topic 2: Trigonometric Functions
Topic 3: Counting and Probability
Begins with a review of the basic algebraic concepts and techniques. Simple relation-ships between variable quantities are used to introduce the key concepts of a function and its graph. Radian measure is introduced, and the graphs of the trigonometric functions. The study of probability begins with the introduction of conditional probability and independence. Students further develop their counting techniques in combinatorics in Specialist Mathematics.
Unit 2
Topic 1: Exponential Functions
Topic 2: Arithmetic & Geometric Sequences
Topic 3: Introduction to Differential Calculus
Exponential functions and logarithms their properties and graphs are examined. Arithmetic and geometric sequences are introduced and their recursive definitions. Rates and average rates of change are introduced and the concept of the derivative as an ‘instantaneous rate of change’. The concepts are reinforced numerically, geometrically, and algebraically. This first calculus topic concludes with derivatives of polynomial functions, using the derivative to sketch curves, calculate slopes and equations of tangents, determine instantaneous velocities, and solve optimisation problems.
Unit 3
Topic 1: The Logarithmic Function
Topic 2: Further Differentiation & Application
Topic 3: Integrals
The logarithmic function is studied in more detail. The study of calculus continues with the derivatives of exponential and trigonometric functions and the concept of a second derivative, its meaning and applications. The unit includes integration as a way of calculating areas. The fundamental theorem of calculus as a link between differentiation and integration is emphasised. Derivatives of logarithmic and exponential functions are explored.
Unit 4
Topic 1: Discrete Random Variables
Topic 2: Continuous Random Variables
Topic 3: Interval Estimates for Proportions Simple linear regression is considered for bivariate data. Discrete random variables are introduced, and their uses in modelling random processes involving chance and variation. Continuous random variables are introduced and their applications. Probabilities associated with continuous distributions are calculated using definite integrals. In this unit students are introduced to statistical inference restricted to estimating